Aire des cerfs-volants: Histoire, Types

Sauter à un chapitre clé

En fait, il y en a une ! Dans cet article, nous allons discuter d'une formule qui permet de calculer l'aire des cerfs-volants et observer plusieurs exemples travaillés qui utilisent cette technique.

Récapitulation. Définition d'un cerf-volant

Avant de commencer, commençons par nous rafraîchir la mémoire sur les cerfs-volants. Un cerf-volant est un type de quadrilatère qui possède deux paires de côtés adjacents égaux. Comme tous les autres quadrilatères, il contient 4 côtés, 4 angles et 2 diagonales.

La structure d'un cerf-volant répond aux caractéristiques d'un quadrilatère cyclique. Un quadrilatère cyclique est un quadrilatère dont les quatre sommets sont situés sur un cercle. Il est parfois appelé quadrilatère inscrit. Le cercle qui contient ces quatre sommets sur sa circonférence est appelé cercle circonscrit ou cercle circonscrit. Voici le schéma d'un cerf-volant inscrit dans un cercle.

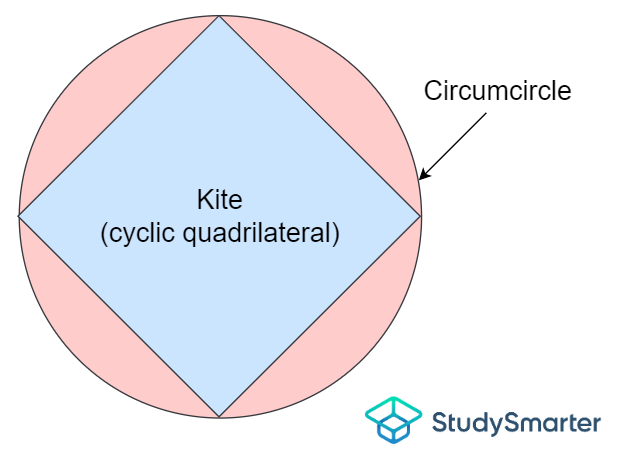
Un cerf-volant inscrit dans un cercle. Un exemple de quadrilatère cyclique.

Exemple de quadrilatère cyclique

Propriétés d'un cerf-volant

Rappelons maintenant les propriétés fondamentales d'un cer f-volant. Nous avons ici un cerf-volant noté ABCD. M est le point d'intersection des diagonales.

Un cerf-volant désigné par ABCD et M est le point d'intersection des diagonales.

Schéma d'un cerf-volant

Le tableau suivant est une liste de ses caractéristiques.

Propriétés d'un cerf-volant	Description
Il possède deux paires de côtés adjacents égaux	AB = BC et AD = DC
Il possède une paire d'angles opposés égaux qui sont obtus	∠BAD = ∠BCD > ^90o
Pas de lignes parallèles
Elle possède deux diagonales non égales	AC ≠ BD
Les diagonales sont perpendiculaires et se coupent en deux	AC ⊥ BD et AM = MC et BM = MD

Nous sommes maintenant prêts à en apprendre davantage sur l'aire d'un cerf-volant.

Formule de calcul de l'aire d'un cerf-volant

La surface d'un cerf-volant est l'espace délimité par ses côtés. Si l'on se réfère à notre schéma précédent d'un cerf-volant, la formule de l'aire est donnée par la formule suivante

\[A=\frac{1}{2}\times d_1 \times d_2\]

où $d_1$ et $d_2$ sont les longueurs de la diagonale verticale et de la diagonale horizontale, respectivement.

$Diagramme d'un cerf-volant avec deux diagonales, l'une horizontale appelée $d_1$ et l'autre verticale appelée $d_2$.$

Surface d'un cerf-volant

Calculer l'aire d'un cerf-volant

Nous avons maintenant une recette explicite pour trouver la surface d'un cerf-volant. Mais comment en est-on arrivé là ? Dans cette partie, nous verrons étape par étape comment cette formule permet de déterminer la surface d'un cerf-volant donné. Encore une fois, portons notre attention sur notre cerf-volant précédent, illustré ci-dessous.

Un cerf-volant désigné par ABCD et M est le point d'intersection des diagonales.

Surface d'un cerf-volant

Pour notre cerf-volant ABCD ci-dessus, appelons la longueur de la diagonale la plus courte $AC=x$ et la longueur de la diagonale la plus longue $BD=y$. D'après les propriétés d'un cerf-volant, ces deux diagonales sont perpendiculaires (à angle droit) et se coupent en deux.

En tenant compte de cela, nous avons

\[AM=MC=\frac{AC}{2}=\frac{x}{2}\]

La surface du cerf-volant ABCD est constituée de la somme de deux surfaces : le triangle ABD et le triangle BCD. En l'écrivant sous forme d'expression, on obtient

Surface du cerf-volant ABCD = Surface de ΔABD + Surface de ΔBCD

Appelons cette équation 1.

L'aire d'un triangle est le produit de sa base et de sa hauteur multiplié par la moitié, c'est-à-dire ,

\[\text{Aire d'un triangle}=\frac{1}{2}\times b \times h\]

où $b$ est la base et $h$ la hauteur. À l'aide de cette formule, déterminons les aires du triangle ABD et du triangle BCD.

\[\text{Aire du triangle ABD}=\frac{1}{2}\times AM\times BD\]

\[\text{Aire du triangle BCD}=\frac{1}{2}\times MC\times BD\]

En remplaçant AM, BD et MC par \N(x\N) et \N(y\N), on obtient

\[\text{Aire du triangle ABD}=\frac{1}{2}\times\frac{x}{2}\times y=\frac{xy}{4}\]

\[\text{Aire du triangle BCD}=\frac{1}{2}\times\frac{x}{2}\times y=\frac{xy}{4}\]

En utilisant l'équation 1, nous obtenons

\[\text{Aire du cerf-volant ABCD}=\frac{xy}{4}+\frac{xy}{4}=\frac{xy}{2}\]

Enfin, en substituant les valeurs de $x$ et $y$, nous obtenons la formule requise pour l'aire d'un cerf-volant.

\[\text{Aire d'un cerf-volant}=\frac{1}{2}\times AC \times BD\]

L'aire d'un cerf-volant et d'un losange

La formule de l'aire d'un cerf-volant suit la même idée que celle de l'aire d'un losange. Rappelons la structure d'un losange. Nous avons ici un losange noté ABCD. M est le point d'intersection des diagonales.

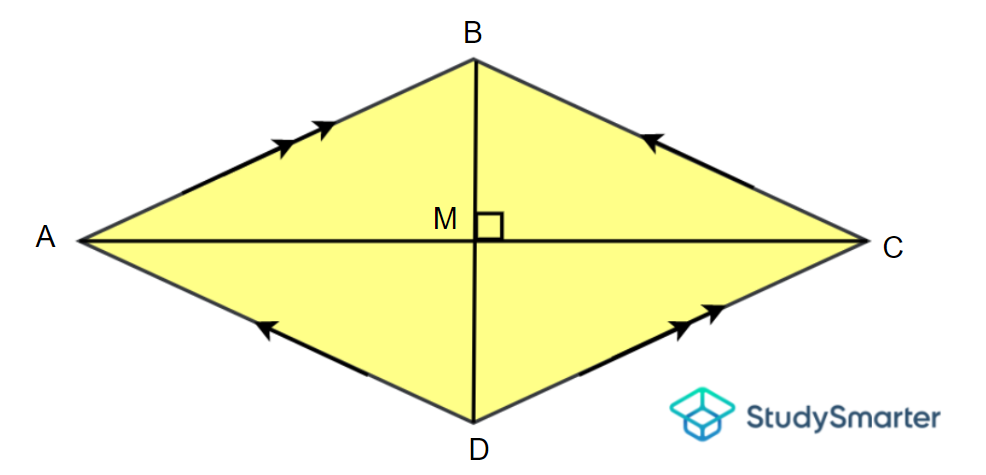
Losange ABCD avec point médian D

Diagramme d'un losange

Tu peux déjà voir les ressemblances avec un cerf-volant, rien qu'en regardant ce diagramme. Le tableau suivant est une liste de ses caractéristiques.

Propriétés d'un losange	Description
A quatre côtés égaux	AB = BC = CD = DA
Possède des angles opposés de mesures égales	∠ABC = ∠CDA et ∠BCD = ∠DAB
Possède deux paires de côtés parallèles	AB // DC et AD // BC
Possède deux diagonales non égales	AC ≠ BD
Les diagonales sont perpendiculaires et se coupent en deux	AC ⊥ BD et AM = MC et BM = MD

Formule de l'aire d'un losange

\[A=\frac{1}{2}\times d_1 \times d_2\]

où _d1 et _d2 sont respectivement les longueurs de la diagonale verticale et de la diagonale horizontale.

$Diagramme d'un losange avec deux diagonales, l'une horizontale appelée $d_1$ et l'autre verticale appelée $d_2$.$

Surface d'un losange

Exemples d'aires de cerfs-volants

Dans cette section, nous allons examiner plusieurs exemples travaillés qui utilisent cette formule permettant de déduire l'aire d'un cerf-volant. Voici le premier exemple.

Cathy possède 3 cartes de notes identiques en forme de cerf-volant dont les diagonales mesurent 5 pouces et 17 pouces. Détermine la somme des aires de ces 3 cartes.

Solution

Les diagonales de chaque boîte sont données par $d_1=5$ et $d_2=17$. En utilisant la formule de calcul de l'aire d'un cerf-volant, l'aire d'une carte est la suivante

\[A=\frac{1}{2}\\N- fois 5 \N- fois 17=\frac{82}{2}=42.5\N]

La surface de chaque cerf-volant est donc de 42,5 ^pouces2. Comme nous avons 3 cartes identiques, il suffit de multiplier cette surface par 3 pour obtenir la surface totale.

\42,5 fois 3 = 127,5 pouces]

Ainsi, la surface totale des 3 cartes est de 127,5 ^po2.

Prenons un autre exemple.

Marie a un carton découpé en forme de cerf-volant. La diagonale la plus courte mesure 3 pieds tandis que la diagonale la plus longue mesure 14 pieds. Quelle est l'aire de ce découpage ?

Elle décide ensuite de diviser ce découpage en 7 morceaux distincts d'aires égales. Quelle serait la surface de chaque morceau ?

Solution

Les diagonales de ce découpage sont données par $d_1=3$ et $d_2=14$. En utilisant la formule de calcul de l'aire d'un cerf-volant, l'aire de ce découpage est la suivante

\N-[A=\frac{1}{2}\Nfois 3 \Nfois 14=\frac{42}{2}=21\N].

L'aire de ce découpage est donc de 21 ^pi2. Puisque Mary veut diviser cette découpe en 7 segments identiques, nous pouvons simplement diviser cette surface par 7 pour identifier la surface de chaque morceau.

\N- [\Nfrac{21}{7}=3\N]

La surface de chaque morceau est donc de 3 ^pi2.

Voici un dernier exemple avant de clore ce sujet.

David a un cerf-volant dont la surface est de 304 pouces carrés. La diagonale la plus courte a une longueur de 16 pouces. Quelle est la longueur de la diagonale la plus longue ?

Solution

Dans cette question, on nous donne les mesures de l'aire et de l'une des diagonales de ce cerf-volant, à savoir $A=304$ et $d_1=16$. Pour trouver la longueur de la diagonale la plus longue, \N(d_2\N), nous devons réarranger la formule donnée pour faire de \N(d_2\N) le sujet. Étant donné que la formule pour la surface d'un cerf-volant est la suivante

\[A=\frac{1}{2}\times d_1 \times d_2\]

En réarrangeant cette formule pour que \ (d_2\) devienne le sujet, on obtient

\[d_2=\frac{2A}{d_1}\]

En substituant maintenant nos valeurs connues pour $A$ et $d_1$, nous obtenons

\[d_2=\frac{2\times 304}{16}=38\]

Ainsi, la longueur de la diagonale la plus longue est de 38 pouces.

Surface des cerfs-volants - Points clés

Uncerf-volant est un type de quadrilatère sans lignes parallèles.
Un cerf-volant a deux paires de côtés adjacents égaux et une paire d'angles opposés égaux qui sont obtus.
Un cerf-volant a deux diagonales non égales.
Les diagonales d'un cerf-volant sont perpendiculaires et se coupent en deux.
La surface d'un cerf-volant est donnée par \[A=\frac{1}{2}\times d_1 \times d_2\] où $d_1$ et $d_2$ sont les longueurs de la diagonale verticale et de la diagonale horizontale, respectivement.