Photosynthesis is the process by which plants, algae, and some bacteria convert light energy into chemical energy stored as glucose. Investigating photosynthesis helps us understand how organisms produce oxygen and food, supporting nearly all life on Earth.
Get started for freeContent creation by StudySmarter Biology Team.
Published: 24.06.2024. Last updated: 01.01.1970.
Un rectangle est un cas particulier de quadrilatère, qui est une figure plane à quatre côtés. Les 4 angles internes d'un rectangle sont tous des angles droits. Un livre, un terrain de football, une fenêtre, une valise de voyage sont tous des exemples de rectangles.
Supposons maintenant que tu veuilles calculer l'espace total couvert par un terrain de football. Tu dois alors savoir comment calculer la surface d' un rectangle.
Un rectangle est un quadrilatère dont les angles internes sont tous des angles droits. L'espace à deux dimensions occupé par un rectangle est la surface d'un rectangle.
Un quadrilatère ayant deux paires de côtés opposés parallèles est appelé un parallélogramme. Puisque tous les angles d'un rectangle sont des angles droits, il s'avère que les paires de côtés opposés d'un rectangle sont toujours parallèles. Cela fait de chaque rectangle un parallélogramme. En fait, le rectangle est considéré comme un type particulier de parallélogramme.
La surface d'un rectangle est la mesure de l'espace qu'il renferme. Elle se calcule en multipliant la longueur du rectangle par sa largeur. L'aire d'un rectangle se calcule en multipliant sa longueur par sa largeur. Considère le rectangle suivant.
Trouve l'aire du rectangle grâce à cet exemple d'illustration.
L'aire d'un rectangle est donnée par la formule :
\[Surface = b \Nfois h\N]
où b = longueur de la base, h = longueur de la hauteur.
La valeur, b, est la longueur du côté AB, qui est considéré comme la base ici. Par convention, l'un des côtés les plus longs du rectangle est considéré comme la base, et l'un des côtés perpendiculaires à la base est considéré comme la hauteur. Dans ce rectangle, la hauteur est égale à la longueur de AD.
Dans certaines conventions, la base et la hauteur sont appelées la longueur et la largeur du rectangle.
Un carré est un cas particulier de rectangle. En plus des 4 angles internes qui sont des angles droits, les 4 côtés d'un carré sont égaux.
Un exemple de l'aire du carré.
Regarde le carré ci-dessus et rappelle la formule de l'aire d'un rectangle : \[Surface = base \Nfois hauteur.\N]
Puisque les 4 côtés d'un carré sont égaux, la base et la hauteur sont égales. Il suffit de connaître la longueur des côtés d'un carré pour calculer sa surface. Ainsi, dans le cas d'un carré, la formule peut être réduite à :
\[Surface = longueur du côté multipliée par la longueur du côté = (longueur du côté)^2].
Lorsque tu étudies la surface d'une figure, , rappelle-toi que la surface est mesurée en unités carrées, telles que les centimètres carrés (cm2), les pieds carrés (ft2), les pouces carrés (in2), etc.
Si tu n'es pas familier avec l'unité carrée, il est utile de considérer le concept tel qu'il est représenté visuellement dans la figure ci-dessous. Réfléchis au nombre d'unités carrées nécessaires pour couvrir exactement et exhaustivement toute la surface d'une figure fermée. Cette quantité est l'aire de la figure.
Unités carrées, Jurgensen & Brown-Géométrie
Les exemples suivants montrent comment trouver l'aire d'un rectangle.
Exemple 1 : Supposons que tu aies un rectangle d'une longueur de 10 unités et d'une largeur de 5 unités. Pour trouver l'aire :
\[Surface = 10 unités, unités fois 5 unités, unités = 50 unités, carré, unités].
Exemple 2 : Imagine une parcelle de jardin ayant la forme d'un rectangle d'une longueur de 15 mètres et d'une largeur de 8 mètres. Détermine la superficie :
\N-[Surface=15\N,mètres\Nfois8\N,mètres=120\N,carrés\N,mètres].
Exemple 3 : Considérons une piscine rectangulaire d'une longueur de 25 mètres et d'une largeur de 10 mètres. Trouve la surface :
\N-[Area=25\N,meters\Ntimes10\N, meters=250\N, square\N, meters].
Voici une explication plus détaillée de la façon de trouver l'aire d'un rectangle :
Un rectangle d'une surface de 60m2 a une base d'une longueur de 20 m. Quelle est la hauteur du rectangle ?
Solution
Surface = b × h
⇒60m2 = 20 m × h
⇒ h = 60m2 ÷ 20 m
⇒ h = 3 m
Si l'on te donne la longueur de 1 des côtés (base ou hauteur) d'un rectangle et la longueur de la diagonale, tu peux calculer la longueur inconnue du côté (hauteur ou base) à l'aide du théorème de Pythagore. Le théorème de Pythagore stipule que dans un triangle à angle droit, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.
La figure suivante montre comment la diagonale d'un rectangle le divise en 2 triangles rectangles, ce qui nous permet d'utiliser le théorème de Pythagore. Ensuite, une fois que la base et la hauteur du rectangle sont connues, la surface peut être calculée.
La diagonale d'un rectangle le divise en 2 triangles à angle droit.
Dans le rectangle ABCD suivant, AB = 9, BD = 15. Trouve l'aire du rectangle.
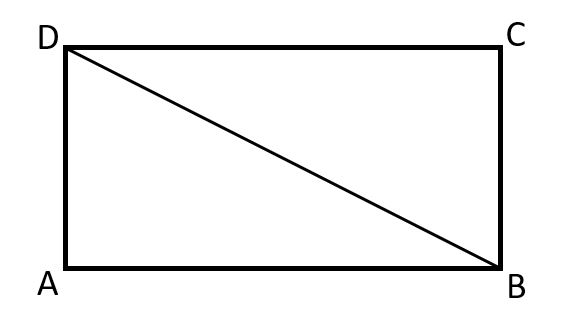
Solution
Puisque les angles internes d'un rectangle sont des angles droits, BD est l'hypoténuse du triangle à angle droit, ΔABD.
Donc ,
D'après le théorème de Pythagore,
\[AD^2 + AB^2 \NFlèche droite AD^2 + 9^2 = 15^2 \NFlèche droite AD^2 = 15^2 - 9^2 \NFlèche droite AD^2 = 144 \NFlèche droite AD = 12 \N]
Surface du rectangle = b × h
= 12 pi. × 9 pi.
= 108 pi2
Un carré a des côtés de 10 pieds de long. Quelle est la surface du carré ?
Solution
Surface = côté × côté
= 10 pi. × 10 pi.
= 100 pi2
Si la longueur et la largeur d'un rectangle sont données sous forme de fractions, tu peux quand même calculer sa surface en multipliant ces fractions.
Prenons un exemple :
Supposons que la longueur \ ( b \N) d'un rectangle soit de \( \frac{3}{4} \N) unités et que la largeur \( h \N) soit de \( \frac{2}{5} \N) unités.
Pour trouver l'aire \( A \N) du rectangle : \N[ A = b \Nfois h \N] Substitue les fractions données : \[ A = \frac{3}{4} \times \frac{2}{5} \] Pour multiplier les fractions : \begin{align*} \text{Multiplier les numérateurs:} & \quad 3 \times 2 = 6 \\\text{Multiplier les dénominateurs:} & \quad 4 \times 5 = 20 \\\N- \n- \n- \n- \n-{align*} Ce qui donne : \[ A = \frac{6}{20} \] Simplifier la fraction en divisant le numérateur et le dénominateur par leur plus grand diviseur commun : \[ A = \frac{3}{10} \] Ainsi, la surface du rectangle est de \( \frac{3}{10} \) unités carrées.
Le périmètre et l'aire sont deux propriétés fondamentales d'un rectangle.
Périmètre d'un rectangle: Le périmètre est la distance totale autour du rectangle, ou la somme de tous ses côtés. Comme les côtés opposés d'un rectangle sont de même longueur, le périmètre \(P\) peut être trouvé à l'aide de la formule : \NP[P=2l+2w\N].
Dans le même exemple, avec une longueur de 5 unités et une largeur de 3 unités, le périmètre serait de
\N- 2(5)+2(3) = 10+6 = 16\N- unités]
En résumé :
où b = base, h = hauteur.
Un carré est un cas particulier de rectangle. En plus des 4 angles internes qui sont des angles droits, les 4 côtés d'un carré sont égaux.
La surface d'un carré est donnée par la formule : Surface = côté × côté
Lorsque les dimensions d'un rectangle sont données en fractions, le processus reste le même : il suffit de multiplier la longueur fractionnaire par la largeur fractionnaire.
At StudySmarter, we have created a learning platform that serves millions of students. Meet the people who work hard to deliver fact based content as well as making sure it is verified.
Gabriel Freitas is an AI Engineer with a solid experience in software development, machine learning algorithms, and generative AI, including large language models' (LLMs) applications. Graduated in Electrical Engineering at the University of São Paulo, he is currently pursuing an MSc in Computer Engineering at the University of Campinas, specializing in machine learning topics. Gabriel has a strong background in software engineering and has worked on projects involving computer vision, embedded AI, and LLM applications.
StudySmarter is a global EdTech platform helping millions of students learn faster and succeed in exams like GCSE, A Level, SAT, ACT, and Abitur. Our expert-reviewed content, interactive flashcards, and AI-powered tools support learners across STEM, Social Sciences, Languages, and more.
Access subjects, mock exams, and features to revise more efficiently. All 100% free!
Get your free account!
