Transformations de similarité

Donnée $∆ABC$ ci-dessous avec les coordonnées$A(2,1),B(2,3),C(5,1)$, un centre de dilatation $(0,0)$et un facteur d'échelle de 2.

Applique la dilatation au polygone et trace le graphique suivant $∆A\text{'}B\text{'}C\text{'}$.

Solution :

Étape 1 : Nous allons commencer par dessiner la pré-image. $∆ABC$.

Étape 2 : D'après la question, nous voyons que le facteur d'échelle est de 2. Remarque que le facteur d'échelle est supérieur à 1. Cela signifie qu'il s'agit d'un agrandissement. Tu multiplies donc chaque coordonnée x et y de $∆ABC$ par le facteur d'échelle, 2. Vois le tableau ci-dessous.

Les figures du graphique ci-dessous représentent des formes avec des coordonnées. $P(2,2),Q(2,4),R(6,4),S(6,2)andW(5,5),X(5,9),Y(12,9),Z(12,5).$ Détermine si elles sont similaires ou non.

Étape 1 : Faire un diagramme

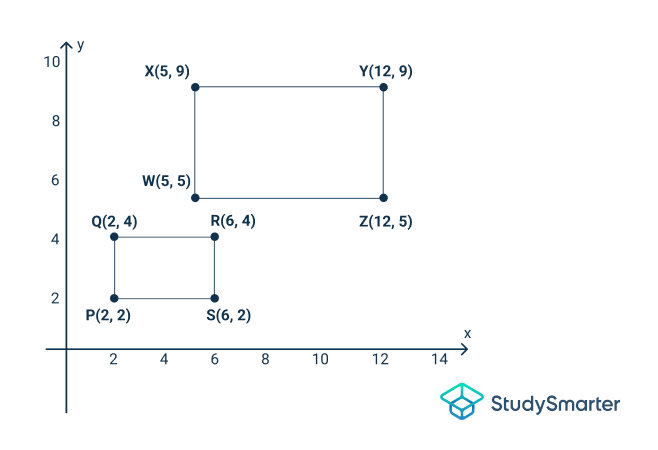
Comme tu peux le voir sur le graphique, les figures ont été dilatées, ce qui signifie qu'une transformation a eu lieu.

Étape 2 : La façon la plus rapide de vérifier leurs similitudes est de comparer les coordonnées des deux figures. La première figure est $PQRS$et la seconde est $WXYZ$. Tout d'abord, nous devons identifier les sommets correspondants. Les rectangles sont tous deux en orientation paysage, nous pouvons donc faire correspondre le bas gauche de l'un au bas gauche de l'autre et ainsi de suite. Tu devrais obtenir que P correspond à W (les deux en bas à gauche), S correspond à Z (en bas à droite), Q à X (en haut à gauche) et R à Y (en haut à droite).

Ensuite, nous vérifions

$\frac{Px}{Wx}=\frac{Py}{Wy}=\frac{Sx}{Sy}=\frac{Zx}{Zy}=\frac{Qx}{Xx}=\frac{Qy}{Xy}=\frac{Rx}{Yy}$

Étape 3 : En introduisant les coordonnées dans l'équation ci-dessus, on obtient

$\frac{2}{5}=\frac{2}{5}\ne \frac{6}{12}\ne \frac{2}{5}=\frac{2}{5}\ne \frac{4}{9}\ne \frac{6}{12}\ne \frac{4}{9}$

Comme tu peux le voir, les coordonnées ne sont pas égales et la similitude n'existe donc pas.

Tu obtiendras le rapport de chaque coordonnée pour voir si elles auront le même facteur d'échelle.

La première série de coordonnées à comparer est $P(2,2)andW(5,5)$. Le rapport sera $\frac{2}{5}:\frac{2}{5}$. Elles sont égales.

Le deuxième ensemble est $Q(2,4)andX(5,9).$ (Le rapport sera $\frac{2}{5}:\frac{4}{9}$. Notre résultat n'est pas égal, ce qui signifie que les chiffres ne peuvent pas être similaires. Si nous avions obtenu $\frac{2}{5}$ au lieu de $\frac{4}{9}$nous aurions continué avec la coordonnée suivante pour voir si nous obtenions un autre $\frac{2}{5}$ comme facteur d'échelle. Le facteur d'échelle étant différent, les figures ne sont pas similaires.

Une autre façon de procéder consiste à examiner le graphique lui-même. Tu dois comparer les côtés correspondants des figures et voir s'ils sont de la même proportion.

D'après la figure, $\overline{PQ}$ est égal à 2 et $\overline{WX}$ est 4. La proportion ici est $\frac{2}{4}$ qui est $\frac{1}{2}$.

$\overline{QR}$ est 4 et $\overline{XY}$ est 7. La proportion ici est $\frac{4}{7}$. $\frac{1}{2}$ est très différente de $\frac{4}{7}$.

Par conséquent, il n'y a pas de similitude.

Détermine si les figures suivantes sont similaires ou non.

Tu ne peux pas vraiment dire si elles sont similaires en les regardant simplement parce qu'elles sont placées dans des positions différentes. Faisons pivoter puis traduisons la première figure et voyons le résultat.

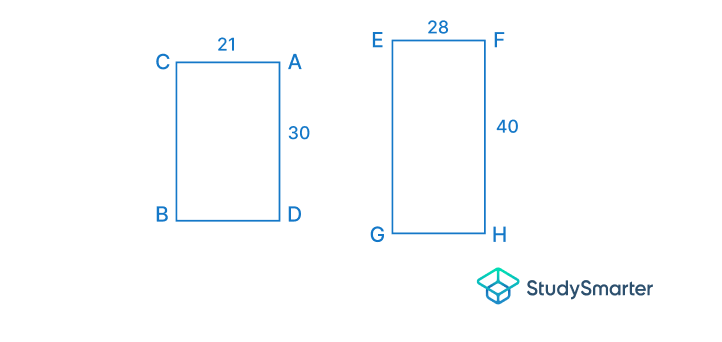
Après la rotation et la translation, on obtient la figure ci-dessus. Comme tu peux le voir, elles ont toutes les deux la même orientation et tu peux maintenant faire des comparaisons en utilisant les pièces correspondantes.

$\frac{30}{40}=\frac{21}{28}=\frac{3}{4}$

Les pièces sont dans les mêmes proportions. Elles sont donc similaires.