Sauter à un chapitre clé
Dans cet article, nous allons nous familiariser avec ces concepts de figuresa> tridimensionnelles et observer comment ils jouent un rôle dans les solides courants que nous pouvons rencontrer dans la vie de tous les jours. Ensuite, nous examinerons les notions de surface, d'aire et de volume pour faciliter la visualisation de ces solides.
Formes en trois dimensions
Contrairement à un objet en deux dimensions,
une figure tridimensionnelle est une figure définie par un espace qui prend en compte trois dimensions : la longueur, la largeur et la profondeur.
Examinons l'exemple ci-dessous.
Nous avons ici un carré. La figure 1 ci-dessous montre un exemple de figure en deux dimensions.
Fig. 1 - Exemple de carré
Remarque que le carré ci-dessus ne comporte que deux dimensions : sa longueur et sa largeur. Essayons maintenant de considérer ce carré comme une figure à trois dimensions. C'est ce qu'on appelle un cube.
Fig. 2 - Exemple de cube
Dans ce cas, nous avons une dimension supplémentaire qui est prise en compte, à savoir la profondeur. La figure 2 ci-dessus montre un exemple de figure tridimensionnelle.
Lesfigures tridimensionnelles sont appelées solides et se composent de trois éléments de base : une face, une arête et un sommet. La section suivante présentera ces termes de manière explicite.
Définition des faces, des arêtes et des sommets
Pour commencer notre discussion principale d'aujourd'hui, nous allons nous familiariser avec trois nouveaux termes, définis ci-dessous.
Laface désigne une surface plane sur un solide. Elle est indiquée par la région ombrée en bleu dans la figure 3 ci-dessous.
Fig. 3 - La face d'un solide
Unearête est un segment de ligne dans lequel deux faces se rencontrent. Elle est indiquée par la ligne bleue (côté) dans la figure 4 ci-dessous.
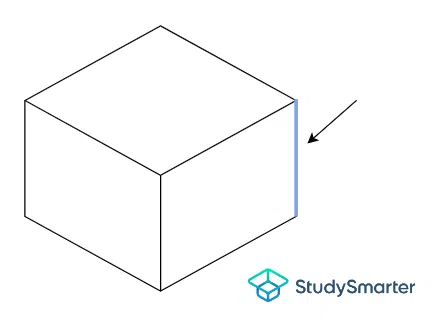
Fig. 4 - L'arête d'un solide
Un sommet (ou coin) est un point où deux arêtes se rencontrent. Il est indiqué par la région encerclée dans la figure 5 ci-dessous.
Fig. 5 - Le sommet d'un solide
La face d'un solide ne doit pas nécessairement s'étendre dans une seule direction, comme celles que tu vois sur le solide ci-dessus. Une face peut s'enrouler autour de l'espace. Peux-tu imaginer cela ?
Lorsque cela se produit, nous disons que nous avons une face incurvée, qui décrit une surface incurvée. Reporte-toi à la flèche de la figure 6 ci-dessous.
Fig. 6 - La face courbe d'un solide
Faces, arêtes et sommets des solides courants
Dans cette section, nous allons nous familiariser avec le nombre de faces, d'arêtes et de sommets de plusieurs solides que nous pourrons rencontrer tout au long de ce programme. Le tableau ci-dessous l'illustre.
Solide | Diagramme | Nombre de faces | Nombre d'arêtes | Nombre de sommets | Nombre de faces courbes |
Sphère |
Sphère | 0 | 0 | 0 | 1 |
Ellipsoïde |
Ellipsoïde | 0 | 0 | 0 | 1 |
Cône |
Cône | 1 | 1 | 1 | 1 |
Cylindre |
Cylindre | 2 | 2 | 0 | 1 |
Tétraèdre |
Tétraèdre | 4 | 6 | 4 | 0 |
Pyramide carrée |
Pyramide carrée | 5 | 8 | 5 | 0 |
Prisme triangulaire |
Prisme triangulaire | 5 | 9 | 6 | 0 |
Cube |
Cube | 6 | 12 | 8 | 0 |
Cuboïde |
Cuboïde | 6 | 12 | 8 | 0 |
Octaèdre |
Octaèdre | 8 | 12 | 6 | 0 |
Prisme pentagonal |
Prisme pentagonal | 7 | 15 | 10 | 0 |
Prisme hexagonal |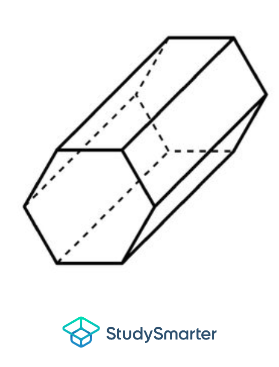
Prisme hexagonal | 8 | 18 | 12 | 0 |
Surface et volume
Tous les solides ont une surface et un volume. Commençons par définir ces termes.
La surface est l'aire totale couverte par toutes les faces d'un solide donné.
Le volume est la quantité d'espace occupée par un solide donné.
Pour te représenter le volume d'un solide, imagine que tu remplis une bouteille d'eau cylindrique, par exemple. La quantité d'eau que cette bouteille peut contenir est le volume de cette forme cylindrique.
La surface peut être trouvée en additionnant toutes les surfaces de chaque face d'une figure tridimensionnelle donnée. Cependant, plutôt que d'exécuter une action aussi lourde, il existe un raccourci !
Chaque solide courant possède une formule particulière pour trouver sa surface. Il en va de même pour son volume. Le tableau ci-dessous présente la formule de la surface et du volume de plusieurs solides notables.
Solide | Diagramme | Surface | Volume | |
Sphère |
Sphère | \[A=4×π×r^2\] | \[V=4×π×\frac{r^3}{3}\] | \(r\) = rayon |
Hémisphère |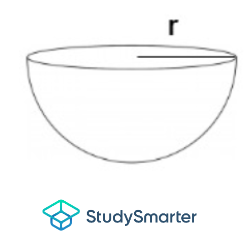
Hémisphère | \[A=3×π×r^2\] | \[V=2×π×\frac{r^3}{3}\] | \N(r\N) = rayon |
Cône |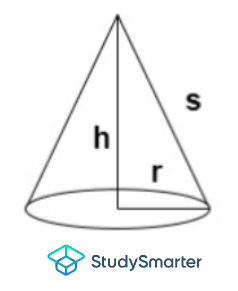
Cône | \[A=π×r×(s+r)\] | \[V=π×r^2×\frac{h}{3}\] | \N-(r\N) = rayon \(s\N-) = hauteur de la pente \(h\) = hauteur |
Cylindre | Cylindre | \[A=2×π×r×(r+h)\] | \[V=π×r^2×h\] | \(r\) = rayon \(h\) = hauteur |
Pyramide |
Pyramide | \N-[A=bl+2bs\N] | \[V=l×b×\frac{h}{3}\] | \N(l\N) = longueur \N(b\N) = base \(h\) = hauteur \(s\N-) = hauteur oblique |
Cube |
Cube | \N- [A=6×l^2\N] | \N- [V=l^3\N] | \N(l\N) = longueur |
Cuboïde |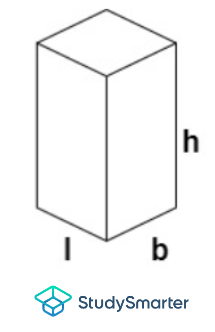
Cuboïde | \N- [A=2×(lb+bn+lh)\N] | \N- [V=l×b×h\N] | \N(l\N) = longueur \N(b\N) = base \N(h\N) = hauteur |
Prisme triangulaire |
Prisme triangulaire | \[A=bh+lb+2ls\] | \[V=l×b×\frac{h}{2}\] | \N(l\N) = longueur \(b\) = base \(h\) = hauteur \(s\N-) = hauteur oblique |
Prisme trapézoïdal |
Prisme trapézoïdal | \[A=(a+b)h+bl+al+2ls\] | \[V=(a+b)×h×\frac{l}{2}\] | \N(l\N) = longueur \(b\) = base \(h\) = hauteur \(s\) = hauteur oblique \(a\) = longueur du sommet |
Prenons deux exemples.
Calcule la surface et le volume d'un cône dont le rayon est de 5 Unités, la hauteur oblique de 8 unités et la hauteur perpendiculaire de 6 unités.
Solution
Les dimensions de ce cône sont données par \(r=5\), \(s=8\) et \(h=6\). En appliquant maintenant la formule de la surface d'un cône, nous obtenons
\[A=π×5×(8+5)=65\pi\approx 641.52\]
Ainsi, ce cône a une surface de 641,52 unités2 correcte à 2 décimales près. Ensuite, nous allons utiliser la formule du volume d'un cône.
\[V=π×5^2×\frac{6}{3}=50\pi\approx 157.08\]
Par conséquent, ce cône a un volume de 157,08unités3 correct à 2 décimales près.
Voici un dernier exemple pour cette section avant de passer à la formule d'Euler.
Quel est le rayon d'une sphère dont la surface est de 67 unités2? Utilise ce résultat pour déterminer également son volume.
Solution
Ici, on nous donne la surface de cette sphère sous la forme \(A=67\). Pour déterminer son rayon, nous devons réarranger la formule de la surface d'une sphère de façon à ce que \(r\) devienne le sujet.
\[A=4×π×r^2\implique r^2=\frac{A}{4\times \pi}\]
Prends maintenant la racine carrée des deux côtés,
\[r=\sqrt{\frac{A}{4\times \pi}}\]
Note que nous ne devons considérer que la racine positive dans ce cas puisque nous avons affaire à des dimensions et des mesures, qui sont toujours considérées comme positives. Nous pouvons maintenant substituer nos valeurs données pour déterminer le rayon.
\[r=\sqrt{\frac{67}{4\times \pi}}=\approx 5.33\]
Le rayon est donc de 5,33 unités, avec une précision de deux décimales. Nous pouvons maintenant utiliser ce résultat pour déterminer le volume de cette sphère. Par souci de précision, nous ne prendrons pas la forme approximative du rayon, mais la forme fractionnaire, c'est-à-dire \(r=\sqrt{\frac{67}{4\times \pi}}\).
\[V=4×π×\frac{\left(\sqrt{\frac{67}{4\times \pi}}\right)^3}{3}\approx 634.87\]
Par conséquent, le volume de cette sphère est de 634,87 unités3.
Formule d'Euler pour un polyèdre
La formule d'Euler stipule que pour tout polyèdre qui ne s'intersecte pas et qui n'a pas de trous, le nombre de faces plus le nombre de sommets moins le nombre d'arêtes est toujours égal à deux. Cela peut s'écrire par l'expression ci-dessous.
\N-[F+V-E=2\N]
où
F = nombre de faces ;
V = nombre de sommets ;
E = nombre d'arêtes.
Application de la formule d'Euler
Dans cette section, nous allons examiner plusieurs exemples d'application de la formule d'Euler. Reporte-toi aux tableaux ci-dessus pour t'aider à vérifier les réponses aux exemples présentés ici.
Faces, arêtes et sommets d'une pyramide à base carrée
Une pyramide à base car rée est un type de pyramide à base carrée. Elle comporte 5 côtés comprenant la base carrée et 4 faces latérales triangulaires congruentes. La figure 7 illustre une pyramide à base carrée.
Fig. 7 - Pyramide à base carrée
Prenons un exemple.
Vérifie que la formule d'Euler est satisfaite pour une pyramide à base carrée.
Solution
D'après notre tableau ci-dessus, une pyramide à base carrée présente les caractéristiques suivantes :
Nombre de faces : 5
Nombre de sommets : 5
Nombre d'arêtes : 8
Maintenant, en appliquant la formule d'Euler, nous obtenons
\[F+V-E=5+5-8=2\]
La formule d'Euler est donc valable pour une pyramide à base carrée.
Faces, arêtes et sommets d'un cuboïde
Un cuboïde est une figure tridimensionnelle délimitée par six faces rectangulaires. Un autre nom pour un cuboïde est un hexaèdre. La figure 8 illustre un cuboïde.
Fig. 8 - Cuboïde
Il existe deux cas particuliers de cuboïdes à considérer.
- Le cuboïde carré : ce type de cuboïde a deux (ou plus) faces carrées opposées.
- Le cube : ce type de cuboïde n'a que des faces carrées.
Voici un exemple.
Vérifie que la formule d'Euler est satisfaite pour un cuboïde.
Solution
D'après notre tableau ci-dessus, un cuboïde présente les caractéristiques suivantes :
Nombre de faces : 6
Nombre de sommets : 8
Nombre d'arêtes : 12
En appliquant la formule d'Euler, nous obtenons maintenant
\[F+V-E=6+8-12=2\]
La formule d'Euler est donc valable pour un cuboïde.
Faces, arêtes et sommets d'un prisme triangulaire
Un prisme triangulaire est un type de prisme composé de deux bases triangulaires et de trois côtés rectangulaires. La figure 9 montre l'image d'un prisme triangulaire.
Fig. 9 - Prisme triangulaire
Voyons maintenant un exemple.
Vérifie que la formule d'Euler est satisfaite pour un prisme triangulaire.
Solution
D'après notre tableau ci-dessus, un prisme triangulaire présente les caractéristiques suivantes :
Nombre de faces : 5
Nombre de sommets : 6
Nombre d'arêtes : 9
Maintenant, en appliquant la formule d'Euler, nous obtenons
\[F+V-E=5+6-9=2\]
La formule d'Euler est donc valable pour un prisme triangulaire.
Faces, arêtes et sommets du prisme hexagonal
Un prisme hexagonal est untype de prisme composé de deux bases hexagonales et six côtés rectangulaires. Il est parfois appelé octaèdre. La figure 10 illustre un prisme hexagonal.
Fig. 10 - Prisme hexagonal
Rappelle qu'un hexagone a six côtés.
Voici un exemple.
Vérifie que la formule d'Euler est satisfaite pour un prisme hexagonal.
Solution
D'après notre tableau ci-dessus, un prisme hexagonal présente les caractéristiques suivantes :
Nombre de faces : 8
Nombre de sommets : 12
Nombre d'arêtes : 18
En appliquant la formule d'Euler, nous obtenons maintenant
\[F+V-E=8+12-18=2\]
La formule d'Euler est donc valable pour un prisme hexagonal.
Faces, arêtes et sommets d'un cylindre
Un cylindre est un type de prisme composé de deux bases circulaires et d'une face incurvée.Il est considéré comme une forme géométrique curviligne. La figure 11 montre un cylindre.
Fig. 11 - Cylindre
Maintenant, remarque qu'uncylindre n'a qu'une seule face incurvée . Il ne s'agit donc pas d'un polyèdre. Cela signifie que la formule d'Euler ne s'applique pas ici.
Vérifions si cela est vrai.
La formule d'Euler s'applique-t-elle à un cylindre ?
Solution
D'après notre tableau ci-dessus, un cylindre présente les caractéristiques suivantes :
Nombre de faces planes : 2
Nombre de faces courbes : 1
Nombre de sommets : 0
Nombre d'arêtes : 2
Tout d'abord, remarque que nous ne pouvons pas insérer le nombre de faces incurvées dans la formule d'Euler car il n'y a pas de variable qui l'indique. Même si nous ne prenions pas en compte cette face courbe et que nous ne tenions compte que des faces planes et des arêtes du cylindre, nous obtiendrions
\[F+V-E=2+0-2=0\]
ce qui n'est certainement pas conforme à la formule d'Euler.
Faces, arêtes et sommets - Points clés à retenir
- La face désigne une surface plane sur un solide.
- Une arête est un segment de ligne sur lequel deux faces se rencontrent.
- Un sommet (ou coin) est un point où deux arêtes se rencontrent.
- La surface est l'aire totale couverte par toutes les faces d'un solide donné.
- Le volume est l'espace occupé par un solide donné.
- La formule d'Euler est donnée par \(F+V-E=2\)
Apprends plus vite avec les 0 fiches sur Faces Edges and Vertices
Inscris-toi gratuitement pour accéder à toutes nos fiches.
Questions fréquemment posées en Faces Edges and Vertices
À propos de StudySmarter
StudySmarter est une entreprise de technologie éducative mondialement reconnue, offrant une plateforme d'apprentissage holistique conçue pour les étudiants de tous âges et de tous niveaux éducatifs. Notre plateforme fournit un soutien à l'apprentissage pour une large gamme de sujets, y compris les STEM, les sciences sociales et les langues, et aide également les étudiants à réussir divers tests et examens dans le monde entier, tels que le GCSE, le A Level, le SAT, l'ACT, l'Abitur, et plus encore. Nous proposons une bibliothèque étendue de matériels d'apprentissage, y compris des flashcards interactives, des solutions de manuels scolaires complètes et des explications détaillées. La technologie de pointe et les outils que nous fournissons aident les étudiants à créer leurs propres matériels d'apprentissage. Le contenu de StudySmarter est non seulement vérifié par des experts, mais également régulièrement mis à jour pour garantir l'exactitude et la pertinence.
En savoir plus