Que sont les fonctions paires ?
Les fonctions paires sont des fonctions comme qui ont les mêmes valeurs lorsque les variables indépendantes négatives comme sont remplacées. C'est pourquoi elles s'expriment le mieux sous la forme suivante: :
En ce qui concerne ce concept, les fonctions sont généralement classées comme étant paires, impaires ou ni l'une ni l'autre.
Confirme que est égal lorsque
Solution :
Puisque
Pour déterminer la nature de cette fonction, nous trouvons en substituant D'où ,
Par conséquent ,
Cela prouve que est une fonction paire pour l'expression
Fonctions impaires
Les fonctions impaires sont des fonctions comme qui ont un équivalent négatif lorsque les variables indépendantes négatives comme sont substituées. Par conséquent, elles s'expriment le mieux sous la forme suivante :
Confirme que f(x) est impair lorsque
Solution :
Puisque
Pour déterminer la nature de cette fonction, nous trouvons en substituant D'où
Lorsque l'on factorise par -1, on obtient
Est-ce que ça te dit quelque chose maintenant ? 😁
Par conséquent ,
Cela prouve que f(x) est une fonction impaire pour l'expression.
Ni l'une ni l'autre des fonctions
Les fonctions ni l'une ni l'autre sont des fonctions comme qui n'ont pas de valeurs équivalentes lorsque les variables indépendantes négatives comme sont substituées. Cela suggère que ce ne sont ni des fonctions paires ni des fonctions impaires. Par conséquent, elles s'expriment le mieux sous la forme suivante :
et
Confirme que est égal lorsque
Solution :
Puisque
Pour déterminer la nature de cette fonction, nous trouvons en substituant D'où ,
L'expression n'est pas équivalente à Par conséquent, il ne s'agit pas d'une fonction paire
Lorsque factorisée par -1
L'expression ci-dessus n'est pas équivalente à , donc ce n'est pas une fonction impaire
Par conséquent ,
et
Cela prouve que n'est ni une fonction pour l'expression
Fonctions paires parmi les identités trigonométriques
Il est possible de déterminer la nature de la fonction (c'est-à-dire paire, impaire ou ni l'une ni l'autre) parmi les identités trigonométriques. Nous utiliserons les deux diagrammes ci-dessous pour l'expliquer.
 Figure 1, une image utilisée pour prouver la nature des fonctions parmi les identités trigonométriques lorsque θ est positif, StudySmarter Originals.
Figure 1, une image utilisée pour prouver la nature des fonctions parmi les identités trigonométriques lorsque θ est positif, StudySmarter Originals.
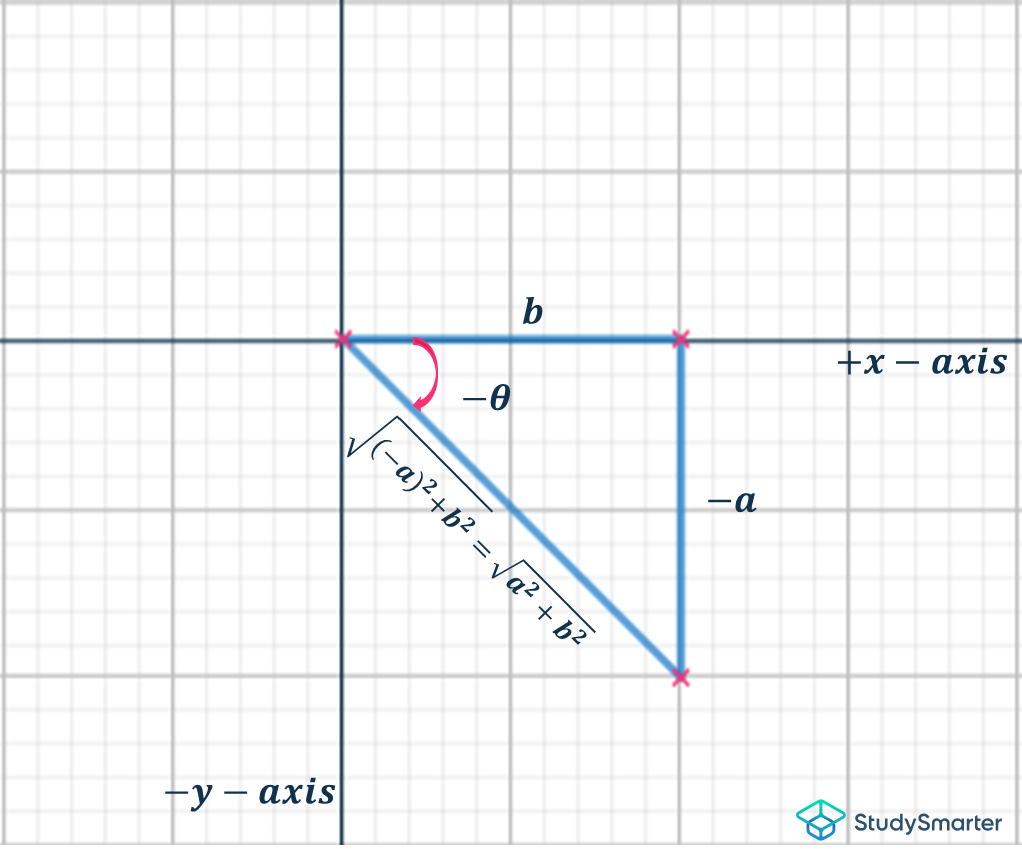
Figure 2, une image utilisée pour prouver la nature des fonctions parmi les identités trigonométriques lorsque θ est négatif, StudySmarter Originals
À partir du premier diagramme, nous pouvons utiliser SOHCAHTOA pour déterminer le cosθ. Si nous faisons cela, nous découvrons que
Mais que se passe-t-il lorsque θ est négatif ? D'après le deuxième diagramme, nous remarquons que bien que le côté opposé (a) ait changé (à -a) parce que la rotation de l'angle se fait dans la direction opposée, le côté adjacent (b) reste constant. Dans ce cas,
D'où,
Quel est le rapport avec les fonctions paires ? Maintenant, si nous exprimons le cosinus comme une fonction de x, de sorte que nous avons cos(x) au lieu de cos(θ). Alors, si
et
Par conséquent ,
Dans ce cas, cela suggère que cos(x) est une fonction paire.
Lesfonctions cosinus sans addition à d'autre(s) fonction(s) sont des fonctions paires.
Qu'en est-il des fonctions sinusoïdales ?
Si tu te réfères à la figure 1, tu en déduiras que
Cependant, lorsque la rotation sur le plan cartésien va dans la direction opposée pour l'angle -θ (comme affiché dans la figure 2), nous remarquons que le côté opposé 'a' dans la figure 1, se transforme en '-a' dans la figure 2 parce que a est situé sur l'axe y négatif. Cela implique que
Si tu factorises par -1, tu obtiendras
D'où ,
Mais quelle est l'utilité de ce détail ? Si nous exprimons le sinus en fonction de x plutôt que de θ, de sorte que nous sachions comment sin(x) ainsi que sin(-x), alors, lorsque
et
avec la factorisation par -1 du côté droit de l'équation, nous arriverions à
Cela signifie sûrement
Cela amène à la soumission que pour la fonction sinus,
mais,
et par implication, nous pouvons conclure que les fonctions sinus ne sont pas des fonctions paires mais des fonctions impaires.
Lesfonctions sin usoïdales qui ne s'ajoutent à aucune autre fonction sont des fonctions impaires.
Pourquoi ne pas jouer avec ces deux diagrammes pour déterminer si les fonctions tangentes sont des fonctions paires, impaires ou ni l'une ni l'autre ?
Si tu cherchais effectivement à déterminer quelles fonctions sont des fonctions tangentes, tu noterais que puisque.
D'après les diagrammes, nous savons également que
Cela implique que
Par conséquent, les fonctions tangentes sont des fonctions impaires.
Quelle est la formule des fonctions paires ?
Pour que nous puissions déterminer la formule des fonctions paires, l'exposant de la variable indépendante, x, est toujours pair avec ou sans constante. Ainsi, pour xn, n est un nombre pair tel que 2, 4, 6...n. Lorsque a, b et c sont des constantes telles que 1, 2, 3... et n un nombre pair, une fonction paire s'exprime alors comme suit
or
Pour les fonctions impaires, l'exposant de la variable indépendante, x, est toujours impair et une constante ne doit pas être présente. Ainsi, pour xn, n est un nombre impair tel que 1, 3, 5...n. Lorsque a et b sont des constantes telles que 1, 2, 3... et n, un nombre impair, une fonction impaire s'exprime comme suit
Pour aucune des deux fonctions, l'exposant de la variable indépendante, x, est à la fois pair et impair avec ou sans la présence d'une constante. Ainsi, pour xn, n est un nombre pair ou impair tel que 1, 2, 3, 4, 5...n. Lorsque a, b et c sont des constantes telles que 1, 2, 3... et n, des nombres pairs ou impairs, alors, aucune fonction ne s'exprime comme suit
ou
ou dans le cas où tous les exposants valeur de la variable indépendante, x, sont impairs avec une constante. Aucune des deux fonctions ne s'exprime sous la forme
où n est un nombre impair.
Graphiques des fonctions paires
Lorsqu'une fonction paire est représentée graphiquement, son graphique est symétrique par rapport à l'axe vertical (axe des y).
Lorsqu'un graphique est symétrique par rapport à un axe, s'il est tourné autour d'un point ou réfléchi sur une ligne, le graphique reste le même, bien que le point sur cet axe soit le même, le point sur l'autre axe porterait un signe opposé parce qu'il s'agit d'une réflexion, tout comme une image dans un miroir.
Ainsi, lorsqu'un graphique est symétrique par rapport à l'axe vertical, les points donnés (p, q) sur ce graphique auraient des points (-p, q) sur ce graphique. Note que la valeur de y (point q sur l'axe vertical) reste inchangée alors que la valeur de x sur le premier point (p) a une valeur opposée pour le second point (-p).
Par exemple la fonction paire
est représentée graphiquement ci-dessous
 Représentation graphique d'une fonction paire, f(x)=x4-2, StudySmarter Originals
Représentation graphique d'une fonction paire, f(x)=x4-2, StudySmarter Originals
D'après le graphique ci-dessus, on voit que les deux points (-1, -1) et (1, -1) du graphique prouvent la symétrie par rapport à l'axe des ordonnées pour la fonction paire
Quelle est la différence entre les fonctions paires et les fonctions impaires ?
Les fonctions paires et les fonctions impaires diffèrent de deux façons principales : dans leurs graphiques et dans leur expression générale.
Différence dans le graphique
Nous venons de voir que le graphique des fonctions paires est symétrique par rapport à l'axe vertical (axe des y).
Mais pour une fonction impaire, son graphique est symétrique par rapport à l'origine. Cela signifie que si l'on fait pivoter la courbe de 180° à l'origine (0, 0), le graphique reste le même.
Cette rotation peut être réalisée en choisissant les points (b, 0) et (0, b) sur le graphique. Si tu fais glisser le point (b, 0) horizontalement jusqu'au point (-b, 0) et si tu fais glisser le point (0, b) verticalement jusqu'au point (0, -b), tu confirmeras que le graphique est exactement le même. N'est-ce pas étonnant ?
Note que, comme nous l'avons déjà mentionné, dans les graphiques de fonctions paires, si tu choisis un point donné (p, q) sur le graphique, tu auras sûrement un autre point sur le côté horizontal opposé de la courbe, qui sera (-p, q).
Tu peux te référer au graphique de x4-2 comme exemple.
Par ailleurs, dans les fonctions impaires, si tu choisis un point (p, q), tu auras un point (-p, -q) sur les axes vertical et horizontal opposés. Par exemple, le graphique de la fonction impaire de
marque les points (2, 8) vers le haut à droite ainsi qu'un autre point (-2, -8) qui est vers le bas à gauche.
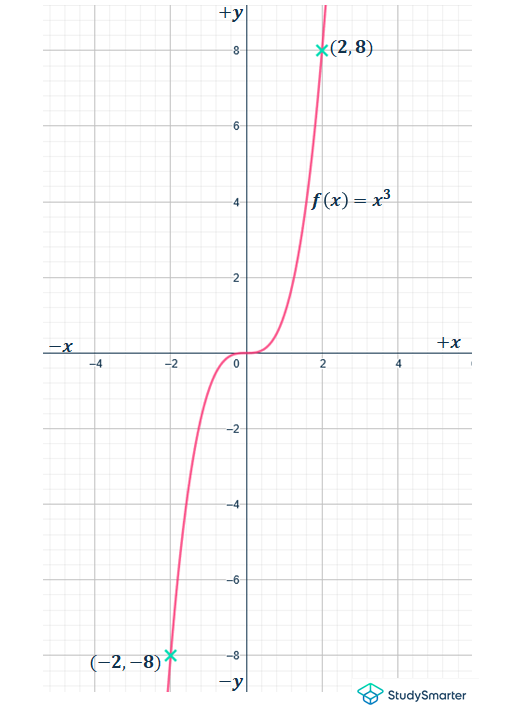
Représentation graphique d'une fonction impaire, f(x)
=x3, StudySmarter Originals
Expression générale
Les fonctions paires se distinguent également des fonctions impaires par leur expression générale. Les fonctions paires sont exprimées de manière à se conformer à la règle.
Cependant, les fonctions impaires n'obéissent pas à cette car dans leur cas,
Au lieu de cela, leurs fonctions sont généralement exprimées de manière à se conformer à la règle
Exemples de fonctions paires
Pour mieux comprendre les fonctions paires, il est conseillé de s'entraîner à résoudre quelques problèmes.
Pour la fonction
Détermine si c'est une fonction paire. Trace le graphique et choisis deux points quelconques pour prouver qu'il s'agit ou non d'une fonction paire.
Solution :
La première tâche consiste à déterminer s'il s'agit d'une fonction paire. Si tu appliques la formule de la fonction paire expliquée plus tôt, en regardant l'expression nous pouvons conclure qu'il s'agit d'une fonction paire puisque tous les exposants de x, c'est-à-dire 6, 4 et 2, sont tous des nombres pairs. Néanmoins, pour obtenir une confirmation supplémentaire, il suffit d'appliquer la règle :
En substituant -x à l'expression, nous obtenons
Ainsi ,
Nous pouvons donc affirmer que l'expression ci-dessus est bien une fonction paire.
La tâche suivante consiste à tracer le graphique et, à l'aide de deux points, à prouver que cette expression est bien une fonction paire.
 Utiliser des points sur un graphique pour prouver les fonctions paires, StudySmarter Originals
Utiliser des points sur un graphique pour prouver les fonctions paires, StudySmarter OriginalsSur le graphique de l'expression ci-dessus, nous avons choisi deux points, (-1, 3) et (1, 3). Cela prouve que l'expression est une fonction paire puisque la paire (-1, 3) et (1, 3) est conforme à (p, q) et (-p, q).
Si
et
Détermine la classe de la somme des deux fonctions.
Solution :
Déterminons maintenant la nature de la somme. Soit h(x) la somme, de sorte que,
Par conséquent, la somme de f(x) et g(x), qui sont toutes deux des fonctions paires, nous donne h(x), qui est une autre fonction paire.
Fonctions paires - Principaux enseignements
- Les fonctions paires sont des fonctions comme f(x) qui ont les mêmes valeurs lorsque les variables indépendantes négatives comme f(-x) sont substituées.
- Les fonctions impaires sont des fonctions comme f(x) qui ont l'équivalent négatif lorsque les variables indépendantes négatives comme f(-x) sont substituées.
- Les fonctions nulles sont des fonctions comme f(x) qui n'ont pas de valeurs équivalentes lorsque les variables indépendantes négatives comme f(-x) sont substituées.
- Il est possible de déterminer la nature de la fonction (c'est-à-dire paire, impaire ou ni l'une ni l'autre) parmi les identités trigonométriques. Les fonctions cosinus sont paires tandis que les fonctions sinus sont impaires.
- Pour que nous puissions déterminer la formule des fonctions paires, l'exposant de la variable indépendante, x, est toujours pair avec ou sans constante.
- Lorsqu'une fonction paire est représentée graphiquement, son graphique est symétrique par rapport à l'axe vertical (axe des y).
- Les fonctions paires et les fonctions impaires diffèrent de deux façons principales : dans leurs graphiques et dans leur expression générale.















