What is Investigating Méthodes Itératives?

Résoudre une équation par une méthode itérative, c'est effectuer un processus pour se rapprocher d'une valeur. On nous donne une valeur initiale approximative, puis nous devenons de plus en plus précis. Cela nous rapproche de la valeur réelle et s'avère nécessaire lorsque nous ne disposons pas d'une méthode directe pour résoudre les racines de l'équation.

Utilisation de la méthode itérative

Une méthode itérative peut être utilisée pour trouver une valeur de $x$ lorsque $f\left(x\right)=0$. Pour effectuer cette itération, nous devons d'abord réarranger la fonction.

Pour ce faire, nous devons réarranger la fonction $f\left(x\right)=0$ en $x=g\left(x\right)$. Par conséquent, nous devons faire de $x$ le sujet de $f\left(x\right)=0$. Cependant, il n'est pas important que nous ayons $x$ termes restants de l'autre côté.

En effet, nous pouvons effectuer $x_{n+1}=g\left(x_n\right)$ce qui signifie que nous prenons notre valeur de $x$ et l'itérer.

Examinons deux exemples pratiques ci-dessous.

Exemples pratiques de calcul par itération

Prenons un exemple plus difficile.

Comment voit-on les méthodes itératives sur un graphique ?

Les méthodes itératives permettent de se rapprocher de plus en plus de la racine d'une équation. Nous les utilisons lorsque nous ne pouvons pas résoudre directement les équations avec d'autres méthodes.

Plus la valeur de $n$ dans $x_n$est élevée, plus nous nous rapprochons de la racine de cette équation, car nous effectuons ce processus de plus en plus souvent.

Nous pouvons voir cela sur un graphique de deux façons : un diagramme en escalier ou un diagramme en toile d'araignée.

Diagrammes en escalier

Un diagramme en escalier fonctionne pour une fonction qui converge directement vers une racine, ce qui signifie qu'à partir de $x_0$nous augmentons ou diminuons directement notre racine avec chaque valeur itérative.

Reprenons notre exemple initial $f\left(x\right)=x^2-3x-5$.

Nous nous concentrerons uniquement sur la racine positive (celle de droite).

Un graphique de $f\left(x\right)=x^2-3x-5$

Nous savons par réarrangement que $x=\sqrt{3x+5}$quand$f\left(x\right)=0$ . Par conséquent, si nous traçons les lignes $y=x$ et $y=\sqrt{3x+5}$l'intersection est la racine de cette équation.

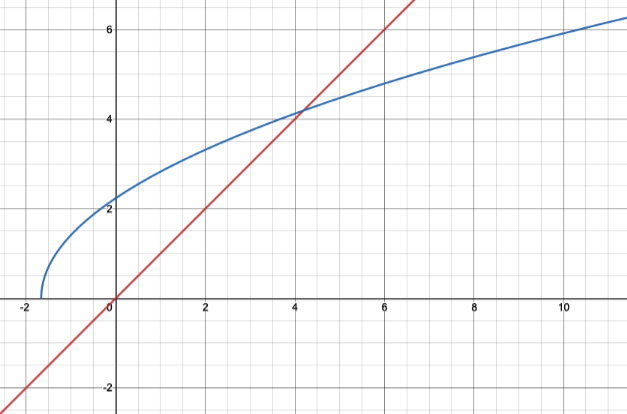
Une intersection entre les lignes $y=x$ et$y=\sqrt{3x+5}$

Traçons maintenant nos points pour $x_0,x_1,x_2$ et $x_3$.

Valeurs $x_0,x_1,x_2,x_3$ marqué.

Alt-text : Valeurs marquées sur le graphique.

Voici une version plus zoomée et nous pouvons voir que ces points convergent lentement vers l'intersection. Si nous ajoutons quelques lignes, nous pouvons voir notre escalier.

Un diagramme d'escalier reliant tous les points susmentionnés.

Si nous continuons et utilisons plus de valeurs, nous nous rapprocherons de plus en plus de cette intersection. Nous ne l'atteindrons jamais réellement mais nous pouvons l'obtenir en vue d'une grande précision.

Diagrammes en toile d'araignée

Un diagramme en toile d'araignée apparaît lorsque nous convergeons vers une racine dans plus d'une direction, ce qui signifie que nos valeurs deviennent à la fois trop élevées et trop basses autour de la racine.

Notre deuxième exemple $f\left(x\right)=x{e}^{-x}-x+3$ illustre ce phénomène. Nous allons nous concentrer sur la racine négative, celle qui se trouve à gauche.

Légende de l'image

Un croquis du graphique $f\left(x\right)=x{e}^{-x}-x+3$

Une fois de plus, en réarrangeant, nous savons que $x=-\ln (1-\frac{3}{x})$lorsque $f\left(x\right)=0$. Nous pouvons donc tracer les lignes $y=x$ et $y=-\ln (1-\frac{3}{x})$et leur intersection est la solution de l'équation $f\left(x\right)=0$.

Intersection entre les lignes $y=x$ et $y=-\ln (1-\frac{3}{x})$,

Traçons maintenant nos points pour $x_0,x_1,x_2$ et $x_3$.

Points $x_0,x_1,x_2,x_3$ marqués.

On voit bien que ces points ne sont pas dans l'ordre. Nous n'avons donc pas un escalier, mais une toile d'araignée et nous convergeons vers la valeur depuis des directions différentes. Voici à quoi cela ressemble.

Un diagramme en toile d'araignée attachant tous les points marqués.

Nous pouvons voir que cela ressemble à une toile d'araignée, et que cela converge vers une valeur à partir de valeurs supérieures et inférieures à l'intersection.