Qu'est-ce que les règles du triangle en mathématiques?

Les règles du triangle en mathématiques établissent les conditions pour qu'un ensemble de trois segments forme un triangle.

Quelles sont les conditions pour qu'un triangle existe?

Pour qu'un triangle existe, la somme de deux côtés doit toujours être supérieure au troisième côté.

Comment appliquer le théorème de Pythagore dans un triangle?

Dans un triangle rectangle, le carré de l'hypoténuse est égal à la somme des carrés des deux autres côtés.

Quels sont les différents types de triangles?

Les différents types de triangles sont: équilatéral, isocèle et scalène, selon la longueur des côtés, et acutangle, rectangle, et obtusangle, selon les angles.

What is Investigating Règles du triangle?

AI Summary

Photosynthesis is the process by which plants, algae, and some bacteria convert light energy into chemical energy stored as glucose. Investigating photosynthesis helps us understand how organisms produce oxygen and food, supporting nearly all life on Earth.

Get started for free

Access relevant flashcards for Investigating Photosynthesis

Start learning

Deprecated: strtotime(): Passing null to parameter #1 ($datetime) of type string is deprecated in /var/www/html/web/app/themes/studypress-core-theme/template-parts/API/explanations/minimal-design/main-content.php on line 24

Content creation by StudySmarter Biology Team.
Sources verified by

Gabriel Freitas.

Quality reviewed by Gabriel Freitas.
Published: 24.06.2024. Last updated: 01.01.1970.

Il est possible de déduire diverses propriétés et valeurs des triangles à angle droit à l'aide des règles trigonométriques. Mais que se passe-t-il si nous avons affaire à des triangles qui n'ont pas d'angles droits ? Pouvons-nous quand même appliquer la trigonométrie pour trouver diverses propriétés des triangles donnés, comme les angles inconnus, les longueurs ou les surfaces ?

Les règles sur les trianglesa> dont il est question dans cet article permettront d'explorer cette question plus en détail :

Règles du triangle - règle du sinus

La première règle du triangle dont nous allons parler s'appelle la règle du sinus. La règle du sinus peut être utilisée pour trouver les côtés ou les angles manquants dans un triangle.

Considère le triangle suivant dont les côtés sont a, b et c, et les angles, A, B et C.

Règle du sinus du triangle - StudySmarter Triangle avec les côtés a, b et c, et les angles, A, B et C, Nilabhro Datta - StudySmarter Originals

Il existe deux versions de la règle du sinus.

Pour le triangle ci-dessus, la première version de la règle du sinus stipule :

$\frac{a}{\sin (A)} = \frac{b}{\sin (C)} = \frac{c}{\sin (C)}$

Cette version de la règle du sinus est généralement utilisée pour trouver la longueur d'un côté manquant.

La deuxième version de la règle du sinus est la suivante :

$\frac{\sin (A)}{a} = \frac{\sin (B)}{b} = \frac{\sin (C)}{c}$

Cette version de la règle du sinus est généralement utilisée pour trouver un angle manquant.

Pour le triangle suivant, trouve un.

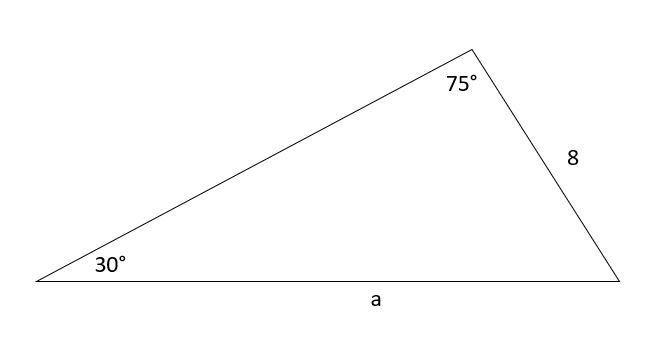
Solution

Selon la règle du sinus,

$\frac{a}{\sin (A)} = \frac{b}{\sin (B)} \frac{a}{\sin (75)} = \frac{8}{\sin (30)} \frac{a}{0.966} = \frac{8}{0.5} a = 15.455$

Lis les règles du sinus et du cosinus pour en savoir plus sur la règle du sinus.

Pour ce triangle, trouve x.

Solution

Selon la règle du sinus,

$\frac{\sin (A)}{a} = \frac{\sin (B)}{b} \frac{\sin (x)}{10} = \frac{\sin (50)}{15} \frac{\sin (x)}{10} = \frac{0.766}{15} \Rightarrow x = 30.71 °$

Règles du triangle - règle du cosinus

La deuxième règle du triangle dont nous allons parler s'appelle la règle du cosinus. La règle du cosinus peut être utilisée pour trouver les côtés ou les angles manquants dans un triangle.

Considère le triangle suivant dont les côtés sont a, b et c, et les angles, A, B et C.

Règle du sinus du triangle - StudySmarter

Triangle avec les côtés a, b et c, et les angles, A, B et C, Nilabhro Datta - StudySmarter Originals

Il existe deux versions de la règle du cosinus.

Pour le triangle ci-dessus, la première version de la règle du cosinus est la suivante :

a² = b² + c² - 2bc - cos (A)

Cette version de la règle du cosinus est généralement utilisée pour trouver la longueur d'un côté manquant lorsque tu connais les longueurs des deux autres côtés et l'angle qui les sépare.

La deuxième version de la règle du cosinus est la suivante :

$\cos (A) = \frac{b ² + c ² - a ²}{2 b c}$

Cette version de la règle du cosinus est généralement utilisée pour trouver un angle lorsque les longueurs des trois côtés sont connues.

Trouve x.

Solution

Selon la règle du cosinus,

a² = b² + c² - 2bc - cos (A)

=> x² = 5² + 8² - 2 x 5 x 8 x cos (30)

=> x² = 19.72

=> x = 4.44

Pour le triangle suivant, trouve l'angle A.

Solution

Selon la règle du cosinus,

$\cos (A) = \frac{b ² + c ² - a ²}{2 b c} \Rightarrow \cos (A) = \frac{7^{2} + 6^{2} - 5^{2}}{2 \cdot 7 \cdot 6} \Rightarrow \cos (A) = \frac{5}{7} \Rightarrow A = 44.4 °$

Lis les règles du sinus et du cosinus pour en savoir plus sur la règle du cosinus.

Règles des triangles - l'aire d'un triangle

Nous connaissons déjà la formule suivante :

$A r e a o f a t r i a n g l e = \frac{1}{2} \cdot b a s e \cdot h e i g h t$

Mais que se passe-t-il si nous ne connaissons pas la hauteur exacte du triangle ? Nous pouvons également déterminer la surface d'un triangle dont nous connaissons la longueur de deux côtés quelconques et l'angle qui les sépare.

Considère le triangle suivant :

La surface du triangle ci-dessus peut être trouvée en utilisant la formule :

$A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} b c \cdot \sin (A) = \frac{1}{2} a c \cdot \sin (B)$

Trouve la surface du triangle.

Solution

$A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} \cdot 6 \cdot 7 \cdot \sin (45) = 14.85$

La surface du triangle est de 10 unités. Trouve l'angle x.

Solution

$A r e a = \frac{1}{2} a b \cdot \sin (C) \Rightarrow 10 = \frac{1}{2} \cdot 5 \cdot 8 \cdot \sin (x) \Rightarrow \sin (x) = 0.5 \Rightarrow x = 30 °$

Clique sur Aire des triangles pour approfondir la règle de l'aire des triangles.

Règles du triangle - points clés à retenir

Tu peux utiliser la règle du sinus pour trouver les côtés ou les angles manquants dans un triangle.
La première version de la règle du sinus stipule que :
$\frac{a}{\sin (A)} = \frac{b}{\sin (C)} = \frac{c}{\sin (C)}$
La deuxième version de la règle du sinus stipule que
$\frac{\sin (A)}{a} = \frac{\sin (B)}{b} = \frac{\sin (C)}{c}$
Tu peux utiliser la règle du cosinus pour trouver les côtés ou les angles manquants dans un triangle.
La première version de la règle du cosinus stipule que :
a² = b² + c² - 2bc - cos (A)
La deuxième version de la règle du cosinus stipule que :
$\cos (A) = \frac{b ² + c ² - a ²}{2 b c}$
Nous pouvons trouver la surface d'un triangle dont nous connaissons la longueur de deux côtés quelconques et l'angle entre eux à l'aide de la formule suivante : $A r e a = \frac{1}{2} a b \cdot \sin (C) = \frac{1}{2} b c \cdot \sin (A) = \frac{1}{2} a c \cdot \sin (B)$

How we ensure our content is accurate and trustworthy

At StudySmarter, we have created a learning platform that serves millions of students. Meet the people who work hard to deliver fact based content as well as making sure it is verified.

Content Quality Monitored by:

Gabriel Freitas

AI Engineer at StudySmarter

Gabriel Freitas is an AI Engineer with a solid experience in software development, machine learning algorithms, and generative AI, including large language models' (LLMs) applications. Graduated in Electrical Engineering at the University of São Paulo, he is currently pursuing an MSc in Computer Engineering at the University of Campinas, specializing in machine learning topics. Gabriel has a strong background in software engineering and has worked on projects involving computer vision, embedded AI, and LLM applications.

Go beyond learning with StudySmarter

Explore thousands of jobs and companies.

Land your dream job →

Find a degree & university that meets your goals.

Find opportunities →

StudySmarter is a global EdTech platform helping millions of students learn faster and succeed in exams like GCSE, A Level, SAT, ACT, and Abitur. Our expert-reviewed content, interactive flashcards, and AI-powered tools support learners across STEM, Social Sciences, Languages, and more.

Sign up for our free learning platform!

Access subjects, mock exams, and features to revise more efficiently. All 100% free!

Get your free account!

What is Investigating Règles du triangle?

AI Summary

Access relevant flashcards for Investigating Photosynthesis

Règles du triangle - règle du sinus

Solution

Solution

Règles du triangle - règle du cosinus

Solution

Solution

Règles des triangles - l'aire d'un triangle

Solution

Solution

Règles du triangle - points clés à retenir

How we ensure our content is accurate and trustworthy

Content Quality Monitored by:

Popular topics in Mathématiques

Popular topics in Règles du triangle

Go beyond learning with StudySmarter

Explore thousands of jobs and companies.

Find a degree & university that meets your goals.

About StudySmarter

Sign up for our free learning platform!