Zur App

Segment de cercle

Un segment de cercle est la zone définie par une ligne allant d'un côté de la circonférence à l'autre.

C'est parti

Fact Checked Content
Last Updated: 01.01.1970
reading time:6 min

Content creation process designed by
Content cross-checked by
Content quality checked by

Les segments sont divisés en segments majeurs et mineurs :

Les segments majeurs représentent la plus grande partie du cercle.
Les segments mineurs représentent la plus petite partie du cercle.

Segment d'un cercle Diagramme des segments majeurs et mineurs StudySmarter

Envie de voir ce contenu et d’autres visuels trop cools?

Inscris-toi ici gratuitement

Segment majeur et mineur d'un cercle -StudySmarter Originals

Lorsque tu travailles sur l'aire d'un segment de cercle, tu dois toujours te rappeler la formule de l'aire d'un cercle : $π \times r^{2}$ . C'est cette formule que tu utilises, que l'angle soit en radians ou en degrés.

Unités pour l'angle du segment d'un cercle

Lorsque tu calcules la surface ou la circonférence d'un segment de cercle, l'angle au centre du cercle qui définit le segment peut être exprimé en radians ou en degrés.

Les degrés sont et sont désignés par $^{\circ}$ . En degrés, une rotation complète est égale à $360^{\circ}$ .
Les radians sont un autre type d'unité pour les angles. Ils sont définis par le rapport entre le rayon du cercle et la longueur de l'arc de cercle et sont désignés par . $^{r}$ . En radians, une rotation complète est égale à $2 π^{r}$ .

Trouver l'aire d'un segment de cercle lorsque l'aire est en radians

Pour trouver l'aire d'un segment de cercle (la partie bleue), tu dois connaître l'angle au centre où les rayons mettent entre parenthèses la corde (x) et le rayon :

Segment d'un cercle diagramme d'un triangle avec l'angle du segment StudySmarter

Envie de voir ce contenu et d’autres visuels trop cools?

Inscris-toi ici gratuitement

Triangle formé à partir de l'angle définissant le segment - StudySmarter Originals

Formules pour trouver l'aire d'un segment de cercle lorsque l'angle est en radians.

Pour trouver la surface d'un segment mineur d'un cercle lorsque l'angle au centre (x) est en radians, la formule est la suivante :

$M i n o r s e g m e n t = \frac{1}{2} \times r^{2} \times (x - \sin (x))$

Pour trouver l'aire d'un segment majeur d'un cercle lorsque l'angle au centre est en radians, la formule est la suivante :

$M a j o r s e g m e n t = (π \times r^{2}) - [\frac{1}{2} \times r^{2} \times (x - \sin (x))]$

Au lieu d'essayer de te souvenir des deux formules, il serait peut-être plus facile de se souvenir de la formule de l'aire du segment principal comme d'une équation de mots :

$M a j o r S e g m e n t = a r e a o f a c i r c l e - a r e a o f m i n o r s e g m e n t$

Le cercle A a un segment mineur qui est surligné en rose.

Trouve l'aire du segment mineur.
Trouve l'aire du segment majeur.

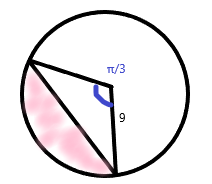
Segment d'un cercle exemple de diagramme de segment StudySmarter

Envie de voir ce contenu et d’autres visuels trop cools?

Inscris-toi ici gratuitement

a. Trouver le segment mineur

Commence par définir les caractéristiques du segment : $R a d i u s = 9; A n g l e = \frac{π}{3}$
Substitue dans la formule :

M i n o r s e g m e n t = \frac{1}{2} \times r^{2} \times (x - \sin (x))

M i n o r s e g m e n t = \frac{1}{2} \times 9^{2} \times (\frac{π}{3} - S i n (\frac{π}{3}))

Segment mineur = 7,64 unités carrées (3 pi²).

b. Trouver l'aire du segment principal

N'oublie pas de trouver le segment majeur ; tu soustrais le segment mineur de l'aire du cercle.

M a j o r s e g m e n t = (π \times r^{2}) - [\frac{1}{2} \times r^{2} \times (x - Sin (x))]

$M a j o r S e g m e n t = (π \times 9^{2}) - [\frac{1}{2} \times 9^{2} \times (\frac{π}{3} - Sin (\frac{π}{3}))]$

Segment principal = 247 unités carrées (3 pi2)

Pour vérifier, si tu additionnes le segment mineur et le segment majeur, tu devrais obtenir à peu près la même surface que celle du cercle entier. $(π \times r^{2})$ . Ici , $(π \times 9^{2}) = 254.47 s q u a r e u n i t s$ et segment mineur + segment majeur = $7.34 + 247 \approx 254.54 s q u a r e u n i t s$ .

Encuentra materiales de estudio relevantes y prepárate para el día del examen

Inscris-toi gratuitement

Trouver la surface d'un segment de cercle lorsque l'angle est en degrés

Tu dois toujours connaître le rayon et le centre du cercle, mais il existe maintenant une formule différente.

Formules pour trouver l'aire d'un segment de cercle lorsque l'angle est en degrés.

La formule pour trouver le segment mineur d'un cercle, lorsque l'angle au centre (x) est en degrés :

$M i n o r s e g m e n t = (\frac{x \times π}{360} - \frac{\sin (x)}{2}) \times r^{2}$

Pour trouver le segment principal d'un cercle lorsque l'angle au centre (x) est en degrés, la formule est la suivante :

$M a j o r s e g m e n t = (π \times r^{2}) - [(\frac{x \times π}{360} - \frac{\sin (x)}{2}) \times r^{2}]$

Utilise le même principe que lorsque l'angle est en radians - tu dois soustraire le segment mineur de toute l'aire du cercle.

Le cercle B a un segment mineur, et l'angle au centre définit la longueur du segment. L'angle est de $120^{\circ}$ et le rayon est de 10 cm.

Quelle est l'aire du segment mineur du cercle B ?
Quelle est l'aire du segment principal du cercle B ?

a. Trouve le segment mineur du cercle B.

Identifie toutes les informations clés nécessaires au calcul de l'aire. Rayon = 10 cm ; angle au centre = $120^{\circ}$
Substitue dans la formule

$M i n o r s e g m e n t = (\frac{π \times x}{360} - \frac{\sin (x)}{2}) \times r^{2}$

$M i n o r s e g m e n t = (\frac{120 \times π}{360} - \frac{\sin (120)}{2}) \times 10^{2}$

Segment mineur = 75,7 unités carrées (3 pi2)

b. Trouve le segment majeur du cercle B.

Substitue les informations clés dans la formule du segment majeur.

M a j o r s e g m e n t = (π \times r^{2}) - [(\frac{x \times π}{360} - \frac{\sin (x)}{2}) \times r^{2}]

M a j o r s e g m e n t = (π \times 10^{2}) - [(\frac{120 π}{360} - \frac{\sin (120)}{2}) \times 10^{2}]

Segment principal = 239 unités carrées (3 pi2)

Únete a tus amigos y haz que estudiar sea divertido

Inscris-toi gratuitement

Longueurs d'arc

La méthode pour calculer la longueur d'arc d'un segment est la même que pour calculer la longueur d'arc d'un secteur.

Pour trouver la longueur de l'arc lorsque l'angle au centre (x) qui définit le segment est en radians :

$A r c L e n g t h = r \times x$

Un segment du cercle C a un rayon de 7 cm et un angle de $20^{\circ}$ . Quelle est la longueur de l'arc de ce segment ?

$A r c l e n g t h = 20^{°} \times \frac{π}{180} \times 7 = \frac{7 π}{9} c m$

Pour trouver la longueur de l'arc lorsque l'angle au centre (x) qui définit le segment est en degrés :

$A r c L e n g t h = x \times r \times \frac{π}{180}$

Un segment du cercle D a un rayon de 5 cm et un angle de $90^{\circ}$ . Quelle est la longueur de l'arc de ce segment ?

$A r c l e n g t h = 90 \times \frac{π}{180} \times 5 = 7.85 c m (3 s . f)$

Segment de cercle - Principaux enseignements

Un segment de cercle est la zone délimitée par la circonférence et la corde. Les segments peuvent être majeurs (la plus grande proportion) ou mineurs (la plus petite proportion).
Pour trouver l'aire d'un segment mineur d'un cercle, tu utilises soit $\frac{1}{2} \times r^{2} \times (x - \sin (x))$ où l'angle (x) est en radians ou $(\frac{x \times π}{360} - \frac{\sin (x)}{2}) \times r^{2}$ où l'angle (x) est en degrés.
Pour trouver l'aire d'un segment majeur, tu soustrais l'aire du segment mineur de l'aire du cercle.
Calculer la longueur de l'arc d'un segment revient à calculer la longueur de l'arc d'un secteur. Pour calculer la longueur de l'arc d'un segment dont l'angle (x) est en radians, tu peux faire ce qui suit $r \times x$ . Si l'angle (x) est en degrés, tu peux utiliser $r \times x \times \frac{π}{180}$ .

S'inscrire avec un e-mail

Tu as déjà un compte ? Connecte-toi

Questions fréquemment posées en Segment de cercle

Qu'est-ce qu'un segment de cercle en mathématiques?

Un segment de cercle est une région plane définie par un arc de cercle et sa corde correspondante.

Comment calcule-t-on la surface d'un segment de cercle?

Pour calculer la surface d'un segment de cercle, on soustrait la surface du triangle formé par la corde de la surface du secteur circulaire.

Quelle est la formule de la corde d'un segment de cercle?

La longueur de la corde d'un segment de cercle est donnée par la formule 2r sin(θ/2), où r est le rayon et θ est l'angle en radians.

Vous avez oublié la troisième question

Pour ajouter un point manquant, veuillez me le préciser et je le fournirai

Sauvegarder l'explication

Découvre des matériels d'apprentissage avec l'application gratuite StudySmarter

Lance-toi dans tes études

À propos de StudySmarter

StudySmarter est une entreprise de technologie éducative mondialement reconnue, offrant une plateforme d'apprentissage holistique conçue pour les étudiants de tous âges et de tous niveaux éducatifs. Notre plateforme fournit un soutien à l'apprentissage pour une large gamme de sujets, y compris les STEM, les sciences sociales et les langues, et aide également les étudiants à réussir divers tests et examens dans le monde entier, tels que le GCSE, le A Level, le SAT, l'ACT, l'Abitur, et plus encore. Nous proposons une bibliothèque étendue de matériels d'apprentissage, y compris des flashcards interactives, des solutions de manuels scolaires complètes et des explications détaillées. La technologie de pointe et les outils que nous fournissons aident les étudiants à créer leurs propres matériels d'apprentissage. Le contenu de StudySmarter est non seulement vérifié par des experts, mais également régulièrement mis à jour pour garantir l'exactitude et la pertinence.